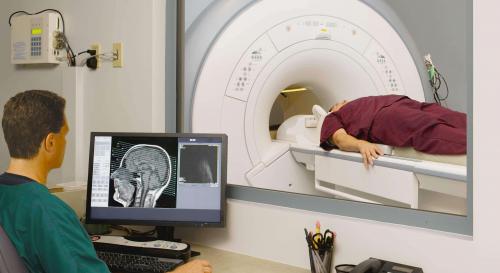
Как определить прямоугольник по его характеристикам

Как определить прямоугольник по его характеристикам

Определение.

Прямоугольник - это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.

Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.

Длинную сторону прямоугольника называют длиной прямоугольника , а короткую - шириной прямоугольника .

Основные свойства прямоугольника

Прямоугольником могут быть параллелограмм, квадрат или ромб.

1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:

AB = CD, BC = AD

2. Противоположные стороны прямоугольника параллельны:

AB||CD, BC||AD

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Сумма углов прямоугольника равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника имеют одинаковой длины:

AC = BD

8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.

10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности

11. Диагональ прямоугольника является диаметром описанной окружности

12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:

∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°

13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника - квадрат).

Связанные вопросы и ответы:

Что такое прямоугольник

Прямоугольник - это четырехугольник , у которого все углы прямые .

На рис. 1 изображен прямоугольник АВСD .

Отрезки АВ и СD , АD и ВС - противолежащие стороны прямоугольника. Противолежащие стороны прямоугольника не имеют общих точек. В прямоугольнике противолежащие стороны равны , тогда на рис. 1 в прямоугольнике АВСD : АВ = DС , АD = ВС .

Отрезки АВ и АD , АD и DC , DC и ВС , АВ и ВС - соседние или смежные стороны. Смежные стороны - стороны, которые имеют общую вершину . Смежные стороны прямоугольника имеют специальные названия: длина и ширина .

Отрезки АС и ВD - диагонали прямоугольника. Диагонали прямоугольника соединяют противолежащие вершины . Диагонали прямоугольника равны и точкой пересечения делятся пополам . Так на рис. 1 АС = ВD и ОА = ОВ = ОС = ОD .

Периметр - это сумма длин всех сторон многоугольника . Обозначается периметр буквой.

Учитывая, что в прямоугольнике противоположные стороны равны, его периметр вычисляется по формуле :или, гдеисмежные стороны прямоугольника (длина и ширина).

Площадь прямоугольника обозначается буквой . Площадь прямоугольника равна произведению его смежных сторон , т.е. еслиисмежные стороны прямоугольника, то его площадь.

Каждая диагональ прямоугольника делит его на два равных треугольника . На рис. 2 ,диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС , т.е. АВС = АDС , а на рис. 2 , б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD , т.е.

ВАD = ВСD .

Прямоугольник, у которого все стороны равны, называют квадратом .

Ось симметрии

Прямоугольник имеет ось симметрии . Ось симметрии прямоугольника - это прямая , проходящая через средины противоположных сторон прямоугольника. У прямоугольника две оси симметрии, на рис. 3 прямые иоси симметрии прямоугольника АВСD .

Если лист бумаги перегнуть по прямым(или), то две части прямоугольника, лежащие по разные стороны от прямой(или), совпадут.

Существуют и другие фигуры, которые имеют ось симметрии, такие фигуры называют симметричными относительно прямой . Так, например, квадрат имеет четыре оси симметрии ( рис. 4 ,), равнобедренный треугольник одну ось симметрии ( рис. 4 , б ), а равносторонний треугольник - три оси симметрии ( рис.4 , в ).

Какие свойства должен иметь прямоугольник

линию, а из нескольких соединенных между собой линий можно получить различныена плоскости и в пространстве. Таким образом, произвольное множество точек позволяет нам создавать геометрическую фигуру. Это может быть квадрат или куб, круг или шар, а также более сложные и неоднозначные фигуры, например, который может быть представлен двумя разными формами.

«Бери и Делай» предлагает узнать, чем отличаются разные виды геометрических фигур.

Плоские геометрические фигуры

Плоская геометрическая фигура располагается в двумерном пространстве, где объектытолько длиной и шириной. Различают следующие фигуры:

• Овал  — это фигура , похожая на яйцо. У нее также нет углов.
• Квадрат  — это, у которой 4 равные стороны и 4 прямых угла.
• Прямоугольник  — это фигура , похожая на квадрат: у нее 4 стороны и они пересекаются под прямым углом. В отличие от квадрата, у прямоугольника только противолежащие стороны равны. Если с помощью отрезка соединить любой угол с противоположным, получится диагональ. И у квадрата, и у прямоугольника диагонали равны.
• Ромб  — это, у которой 4 равные стороны, но пересекаются они не под прямыми углами. У ромба противоположные углы ромба равны. Ромб, так же как квадрат и прямоугольник, является четырехугольником.
• Треугольник  — это фигура , у которой 3 угла и 3 стороны. Точки, в которых пересекаются стороны треугольника, принято называть его.

:

остроугольный —все углыострые (каждый равен менее 90°)

тупоугольный —один уголявляется тупым (равным более 90°)

прямоугольный —один уголявляется прямым (равным 90°)

• Трапеция  — это четырехугольник , у которого как минимум 2 стороны параллельны. Таким образом, квадрат, ромб и прямоугольникрассматривать как частные случаи трапеции.
• Параллелограмм  — четырехугольник , у которого противолежащие стороны попарно параллельны. Так, прямоугольник, квадрат и ромб считаются частными случаями параллелограмма.
• Пентагон  —, представляющая собой правильный многоугольник с 5 сторонами. У пентагона все стороны и углы равны.
• Гексагон  — это правильный многоугольник, у  которого 6 равных сторон, а углы образуют 6 равносторонних треугольников.
• Крест  — это фигура , которая состоит из 2 пересекающихся линий или прямоугольников.
• Звезда  — плоский невыпуклый многоугольник , по форме напоминающий звезду. Звезда может быть трехконечной, четырехконечной, пятиконечной (как на картинке выше) и так далее.

, если ей целиком принадлежат все точки отрезка, соединяющего любые ее две точки. Круг, шар, овал и треугольник являются выпуклыми фигурами. А четырехугольники могут быть как выпуклыми, так и невыпуклыми. К примеру, на картинке выше изображена одна и та же фигура — дельтоид . Это, стороны которого можно сгруппировать в две пары равных смежных сторон. — дельтоид выпуклый, а справа — невыпуклый.

Пространственные геометрические фигуры

Если фигура располагается в трехмерном пространстве, где объектыдлиной, шириной и высотой, а также имеют глубину или толщину, ее называют пространственной. Чаще всего различают следующие пространственные фигуры:

• Конус образован множеством лучей, которые соединяют все точки некоторой плоской кривой с единой точкой пространства (вершиной конуса). Конусы различаются между собой: например, если основанием конуса является круг, то это может быть.
• Цилиндр по  своей форме напоминает валик. В его основании находятся круги, а между ними — часть цилиндрической поверхности.
• Куб  — это многогранная фигура , каждая грань которой представляет собой квадрат. При этом у него 6 граней, 12 ребер и 8 вершин. Куб также можно назвать правильным гексаэдром , или шестигранником.
• Пирамида  — это многогранник , у которого в основании находится многоугольник, а грани представлены треугольниками, имеющими общую вершину.
• Призма  — это многогранник , 2 грани которого являются равными многоугольниками, располагающимися в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. На картинке выше частный пример — шестиугольная призма. У нее 8 граней, 18 ребер и 12 вершин.

, или платоновым телом. В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:

• Тетраэдр, или треугольная пирамида. У этого многогранника гранями являются 4 треугольника.
• Гексаэдр, или куб.
• Октаэдр  — многогранник, чьими гранями являются 8 равносторонних треугольников. Если разрезать октаэдр пополам, можно получить две одинаковые пирамиды.
• Додекаэдр  — многогранник, у которого 12 граней и все они правильные пятиугольники.
• Икосаэдр  — многогранник, гранями которого являются 20 правильных треугольников.

к выпуклому виду, а невыпуклая форма называется большим икосаэдром.

Как отличить прямоугольник от квадрата

Все мы знаем, что прямоугольник – это фигура с четырьмя сторонами и прямыми углами. А вот как найти площадь прямоугольника знают не все, хотя эта формула может пригодиться не только на уроках, но и в жизни, например, при рисовании или во время стройки.

Площадь прямоугольника – что это

Свойства прямоугольника

Полезная информация о площади прямоугольника

Формулы площади прямоугольника

Задачи на нахождение площади прямоугольника

FAQ

Вывод

В этой статье мы расскажем, что из себя представляет площадь прямоугольника, как ее найти и решим несколько задач на нахождение площади.

Площадь прямоугольника – что это

Площадь прямоугольника – это мера, указывающая, сколько плоской поверхности занимает данный геометрический объект. Она определяется умножением длины одной из сторон прямоугольника на длину другой стороны.

Площадь всегда имеет квадратные единицы измерения, так как мы умножаем длину на длину. Например, если стороны прямоугольника измеряются в сантиметрах, то площадь будет выражаться в квадратных сантиметрах.

Площадь прямоугольника является чрезвычайно важной характеристикой при решении множества задач, связанных с геометрией. Она позволяет нам сравнивать и оценивать различные прямоугольники по их размеру. Кроме того, знание площади позволяет нам решать задачи, связанные с распределением материала, площадью помещений или участков земли, проектированием объектов и многими другими.

Свойства прямоугольника

Прямоугольник обладает множеством интересных и полезных свойств, которые делают его одной из наиболее изучаемых и применяемых геометрических фигур.

Рассмотрим основные свойства прямоугольника:

• Наиболее очевидная особенность прямоугольника – это то, что он обладает двумя парами параллельных сторон. Это означает, что противоположные стороны прямоугольника равны и параллельны друг другу. Благодаря этому свойству мы можем использовать прямоугольник для измерения площади и проведения приближенных вычислений.
• Еще одной важной характеристикой прямоугольника является то, что его диагонали равны по величине. Данное свойство позволяет нам определить длину диагонали, если известны размеры сторон, используя теорему Пифагора. Также диагонали прямоугольника делят его на две равные треугольные части, что может быть полезно при решении различных задач.
• Прилегающие стороны прямоугольника всегда строго перпендикулярны, а это значит, что все углы равны 90°, и сумма всех углов составляет 360°
• Прямоугольник обладает симметричными свойствами. Если его разрезать вдоль одного из его диагоналей, получится две равных половины, которые буду симметричны относительно этой оси.
• Прямоугольник может иметь центральную симметрию относительно точки пересечения его диагоналей.
• Прямоугольник хорошо подходит для различных геометрических конструкций. Свойства позволяют использовать его для построения перпендикулярных линий, а также для нахождения центра окружности, вписанной в прямоугольник.

Полезная информация о площади прямоугольника

Вот несколько полезных фактов о площади прямоугольника:

• Без знаний о вычислении площади прямоугольника вам будет сложно сдать любую контрольную как в школе, так и в университете.
• Существует 7 разных формул для вычисления площади, но чаще всего используется только одна.
• Расчет можно сделать, зная, как вычислять площадь прямоугольных треугольников.
• Площадь всегда измеряется в квадратных единицах, например, см².
• Знание формулы для расчета площади прямоугольника поможет рассчитать количество необходимого материала для ремонта.

Формулы площади прямоугольника

Площадь прямоугольника можно вычислить по нескольких формулам. Разберем самые простые и популярные.

Вычисление по длине и ширине сторон

Самая главная формула для вычисления площади прямоугольника:

Вычисление через синус угла

Когда нет данных о длине сторон прямоугольника, используем формулу:

Диагональ соединяет противоположные углы прямоугольника, соответственно знание значения угла и длины одной диагонали достаточно для вычисления площади.

Вычисление по одой стороне и диагонали

Если вы знаете только длину одной из сторон и длину диагонали, рассчитывайте площадь по формуле:

Вычисление через периметр

Если вам известны периметр прямоугольника и длина одной из сторон, воспользуйтесь формулой:

Задачи на нахождение площади прямоугольника

Разберем несколько задач на вычисление площади прямоугольника по разным формулам.

Вычисление по длине и ширине сторон

Допустим, дано: сторона а = 17 см, сторона b = 29 см.

Подставим данные под формулу, чтобы вычислить площадь:

S = 17 * 29

S = 493 см²

Таким образом, площадь прямоугольника составит 493 квадратных сантиметра.

Вычисление через синус угла

В задаче дано, что диагональ d = 18 см., а sin(a) = 30°.

Как определить длину сторон прямоугольника

Урок 15. Математика 5 класс ФГОС

В этом видеоуроке мы узнаем, какую фигуру называют прямоугольником. Рассмотрим элементы прямоугольника. Выясним, что называют периметром прямоугольника. А также поговорим о симметрии.

Получите невероятные возможности

Давайте представим себе такую историю.

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Папа научил меня делать самолётик оригами! – восхищался Саша. – Посмотри, как круто летает такой самолётик!

– Да… его полёт завораживает! – наблюдал за самолётиком Паша. – Только вот я бы уточнил, что искусство создания бумажных самолётиков называется аэрогами или бумажная авиация . Это одна из техник оригами, при которой необходимо не только сложить красивую фигурку, похожую на оригинал, но и предусмотреть её лётные характеристики. Самолёты из бумаги были известны более 2000 лет назад. Однако тогда это были не самолётики, а птички.

Датой создания бумажного самолётика считается 1909 год, но более популярной датой является 1930 год. Тогда основатель известной компании по аэродинамике Lockheed Corporation Джек Нортроп заинтересовался, как из бумаги сделать самолёт.

– А зачем этому человеку нужны были бумажные самолётики? – поинтересовался Паша.

– Изобретатель хотел протестировать на бумажных самолётах свои новые идеи, – продолжил Паша. – Использование бумажной подделки в воздухе помогало правильно подбирать форму для будущих летательных аппаратов.

– Как же это интересно! – с восторгом сказал Саша.

– И это ещё не всё! – продолжил Паша. – В наши дни бумажная авиация, или аэрогами, получила мировую известность. Каждый человек знает, как сложить элементарный самолётик и запустить его. Но на сегодняшний день это уже не просто забава, а серьёзное увлечение, по которому проводят соревнования по всему миру.

– Вот бы мне побывать на таких соревнованиях, – сказал Саша.

– Обязательно побываешь! – подбодрил друга Паша. – Главное верить в свою мечту! Ну и, конечно же, тебе ещё будет полезным познакомиться с условиями создания и схемами бумажных самолётиков. Одними из главных условий создания самолётика являются использование бумаги прямоугольной или квадратной формы и чёткое соблюдение симметрии.

– Ого! – задумался Саша. – Вот про прямоугольные и квадратные формы я всё знаю, а про симметрию совсем ничего, – расстроился он.

– А давай спросим у Электроши, – предложил Паша. – Он точно всё знает!

– Ребята, прежде чем я вам расскажу о прямоугольниках и симметрии, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь поговорим о прямоугольниках, – предложил Электроша. – И сразу начнём с вопроса: как вы понимаете, что такое прямоугольник?

– Прямоугольник – это четырёхугольник, у которого все углы прямые, – ответил Паша.

– Молодец! – похвалил Пашу Электроша. – Посмотрите: на листе изображён прямоугольник ABCD. Вы уже знакомы с элементами многоугольников. Назовите элементы нашего прямоугольника.

– Прямоугольник ABCD имеет 4 вершины: А, B, C и D, 4 одноимённых угла и 4 стороны: AB, BC, CD и DA – ответил Саша.

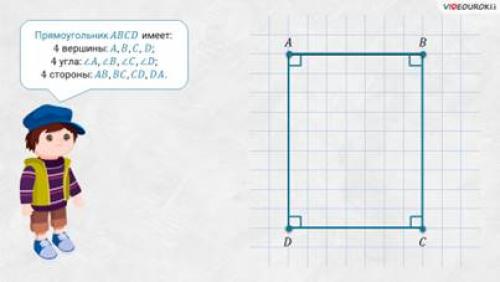
– Всё верно! – подтвердил Электроша. – Посмотрите: стороны AB и BC имеют общую вершину B. Такие стороны называют соседними сторонами прямоугольника ABCD. Также соседними сторонами будут стороны BC и CD с общей вершиной C, CD и DA с общей вершиной D, DA и AB с общей вершиной А.

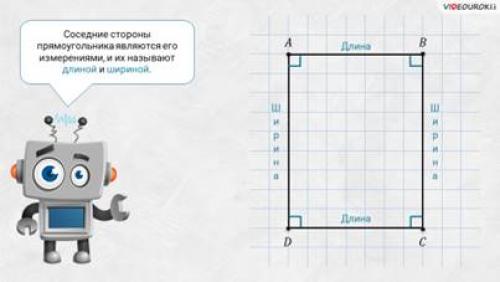
– А что вы можете сказать о сторонах, например, AB и CD нашего прямоугольника ABCD? – спросил у ребят Электроша.

– Стороны AB и CD не имеют общих вершин, – ответили мальчишки.

– Молодцы! – похвалил ребят Электроша. – Такие стороны называют противолежащими сторонами прямоугольника ABCD. Также противолежащими будут стороны BC и AD. Запомните! Противолежащие стороны прямоугольника равны.

– А теперь посмотрите: на листке изображён прямоугольник ABCD, его противолежащие стороны равны. Если длину прямоугольника обозначить буквой а, а ширину – буквой b, то его периметр можно вычислить по формуле: P = 2a + 2b.

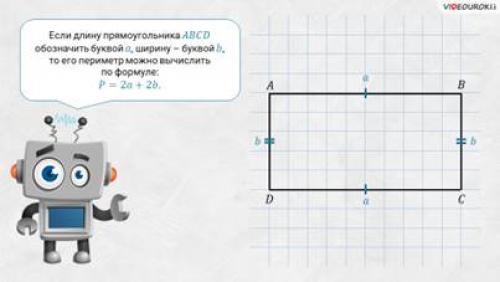
– Среди прямоугольников есть особые, – продолжил Электроша, – у которых все стороны имеют одну и ту же длину. Вы, конечно, помните, что такие прямоугольники называют квадратами . Если длину стороны квадрата обозначить буквой а, то его периметр можно вычислить по формуле: P = 4a.

– А теперь давайте проведём небольшой эксперимент. Возьмите лист бумаги прямоугольной формы и сложите его пополам так, чтобы противолежащие стороны совпали. Затем разверните этот лист. Что вы можете сказать о двух частях, получившихся в результате сгиба листа? – спросил у ребят Электроша.

– Видно, что две части нашего прямоугольного листа, лежащие по разные стороны от линии сгиба, совпадают.

Как определить площадь прямоугольника

         Приведем пример определения центра массы тела методом разделения его на отдельные тела, центры масс которых известны.

Пример 1 . Определить координаты центра массы однородной пластины (рис.9). Размеры заданы в миллиметрах  на рисунке 9.

Решение:   Показываем оси координат и. Разбиваем пластину на части, которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим диагонали, точки пересечения которых и определяют положения центров массы каждого прямоугольника. В  принятой системе координат несложно найти значения координат этих точек. А именно:

(-1; 1),(1;5),(5;9). Площади каждого тела соответственно равны:

 ;;.

Площадь всей пластины равна:

.

         Для определения координат центра массы заданной пластины применяем выражения (21). Подставим значения всех известных величин в  данном уравнении, получим

.

         Согласно полученных значений координат центра массы пластины укажем точку С на рисунке. Как видно, центр массы (геометрическая точка) пластины находится за ее пределами.

Способ дополнения . Этот способ есть частичным случаем способа разделения. Он может применяться к телам, которые имеют вырезы (пустоты). Причем, без  вырезанной части, положение центра массы тела известно. Рассмотрим например применение такого  метода.

Пример 2. Определить положение центра массы веса круглой пластины радиусом  R, в которой есть вырез радиусом  r (рис.10). Расстояние.

.

.