Прямоугольник: основные свойства и простые способы решения задач

Прямоугольник: основные свойства и простые способы решения задач

Тема. Прямоугольник

Цели:

Обучающая:

дать определение «прямоугольника»;

рассмотреть свойства прямоугольника как частного вида параллелограмма;

продолжить формировать умения учащихся применять свойства и признаки параллелограмма при решении задач.

Развивающая:

развивать творческую и мыслительную деятельность, логическое мышление учащихся в процессе изучения нового материала и решения задач;

развивать познавательный интерес и любознательность учащихся, умения самостоятельно работать, излагать мысли грамотным математическим языком.

Воспитательная:

прививать учащимся интерес к предмету;

формировать умения аккуратно и грамотно выполнять математические записи и чертежи;

учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности.

Оборудование: интерактивная доска

Тип урока: урок изучения нового материала

Структура урока

Организационный момент (2 мин.)

Актуализация опорных знаний и умений учащихся (5 мин.)

Проверка домашнего задания (8 мин.)

Мотивация учебной деятельности учащихся (3 мин.)

Изучение нового материала (10 мин.)

Закрепление изученного (10 мин.)

Домашнее задание (3 мин.)

Подведение итогов урока (4 мин.)

Организационный момент

Сообщение темы и целей урока

Актуализация опорных знаний и умений учащихся

повторяем изученный материал по теме:

1. Продолжите предложение:

а) в параллелограмме противоположные стороны … (равны)

б) в параллелограмме противоположные углы … (равны)

с) диагонали параллелограмма точкой пересечения … (делятся пополам)

д) параллелограмм является … (выпуклым четырёхугольником)

е) сумма углов выпуклого четырёхугольника равна … (360)

ж) четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется… (трапеция)

з) существуют такие виды трапеций: … (равнобокие и прямоугольные)

и) прямоугольная трапеция – это трапеция, у которой… (боковая сторона перпендикулярна основаниям).

Связанные вопросы и ответы:

Что такое прямоугольник

Вдля того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силутакже будет равен 90°.

В геометрии доказывается, что две прямые,одной и той же третьей прямой, параллельны между собой. Применив эту теорему к противоположным сторонам прямоугольника, перпендикулярным смежным с ними сторонам, получаем, что противоположные стороны прямоугольника параллельны, поэтому каждый прямоугольник является.

В, где сумма углов четырёхугольника не равна 360°, прямоугольников в указанном приведённым определением смысле не существует, однако можно определить их обобщения.

Какие свойства имеет прямоугольник

Знакомство с периметром и площадью у детей происходит в начальной школе. Часто ребята путают данные определения. Чтобы такого не происходило, предлагаем вникнуть в эту тему и разобраться, как найти периметр и площадь прямоугольника и квадрата.

Что такое периметр

Периметр — это сумма длин сторон многоугольника. Периметр принято обозначать латинской буквой Р.

В чём измеряется периметр :

1. в миллиметрах (мм)
2. сантиметрах (см)
3. дециметрах (дм)
4. метрах (м)
5. километрах (км)

Существуют и другие единицы измерения, но в школе в основном используют именно эти.

Как найти периметр прямоугольника , квадрата и треугольника

Для нахождения периметра необходимо сложить длины всех сторон. Например, нам дан прямоугольник со сторонами 4 см и 5 см.

Чтобы найти периметр этого прямоугольника, мы сложим длины сторон:

4 см + 5 см + 4 см + 5 см = 18 см

Но можно сделать ещё проще. 

Противоположные стороны у прямоугольника равны, поэтому мы можем сложить ширину и длину, а потом просто умножить эту сумму на 2. Для этого воспользуемся формулой:

Р = (4 + 5) * 2 

Р = 18 (см)

Если же нам дан треугольник , то мы просто сложим длины всех его сторон.

А вот с квадратом ещё проще. Так как у квадрата все стороны равны, мы можем длину одной стороны умножить на 4. Так мы узнаем периметр квадрата.

Чтобы эта информация всегда была под рукой, сохраняйте себе памятку, как найти периметры разных фигур.

Что такое площадь

Если простыми словами, то площадь — это внутренняя часть плоской фигуры. Площадь принято обозначать латинской буквой S.

В чём измеряется площадь:

1. в квадратных миллиметрах (мм²)
2. квадратных сантиметрах (см²)
3. квадратных дециметрах (дм²)
4. квадратных метрах (м²)
5. арах (а)
6. гектарах (га)
7. квадратных километрах (км²)

Как найти площадь квадрата

Чтобы найти площадь квадрата, необходимо длину стороны умножить саму на себя.

Как найти площадь прямоугольника

Чтобы найти площадь прямоугольника, необходимо длину стороны умножить на ширину.

Как определить, является ли фигура прямоугольником

Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.

Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d²= a²+ b², а сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон:

где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:

a = √d²— b²

b = √d²— a²

где d — диагональ, а, b — стороны прямоугольника.

Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:

Р = 2a + 2b = 2 (а + b)

Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:

a = (P — 2b) / 2

b = (P — 2a) / 2

Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.

Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:

S = аb

Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:

a = S / b

b = S / a

где S — площадь прямоугольника, a, b — его стороны.

Какие типы прямоугольников существуют

Прямоугольник — плоская фигура, у которой стороны попарно равны и параллельны. Диагонали прямоугольника тоже одинаковые. Одна диагональ делит исходную фигуру на два прямоугольных треугольника с острыми углами по сорок пять градусов. Исходя из этих данных можно легко найти стороны прямоугольника, зная только численное значение диагонали.

Инструкция

Для нахождения сторон прямоугольника нужно рассмотреть один из тех самых прямоугольных треугольников. В нем гипотенуза является диагональю прямоугольника, а катеты — его сторонами. Перед непосредственным вычислением с числовыми значениями нужно найти уравнения в общем виде. Для каждой стороны будет свое уравнение. Итак, для получения формул, в прямоугольном треугольнике обозначьте катеты латинскими буквами а и b, а гипотенузу — с.

Решение задачи заключается в определении синуса и теоремы Пифагора. Выберите любой из острых углов в треугольнике (они равны), с которым будете работать. Определите прилежащий к нему катет и, противолежащий от него, другой катет. Например, пусть, прилежащим к углу, будет катет b, а находящимся напротив — катет а.

Далее, исходя из определения синуса, которое гласит, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, составьте уравнение: sin 45 = а/с. В данном примере, по условию, известны: синус угла (sin 45 ~0,7) и гипотенуза с. Отсюда, получается уравнение 0,7=а/с, из которого а=0,7с. Осталось подставить численное значение с. Найденная сторона а будет равна параллельной стороне в прямоугольнике. Таким образом, известны две стороны фигуры.

Источники:

• Геометрия 7-9 классы. Погорелов. Просвещение 2010 год.

Как найти площадь прямоугольника

Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла. Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой. Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами, квадрат — это особенный случай прямоугольника.

Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно воспользоваться следующей формулой:

a = d * sinα

где d — это диагональ, а, b — одна из сторон фигуры.

Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой стороной — 60º.

Через его площадь и известную сторону

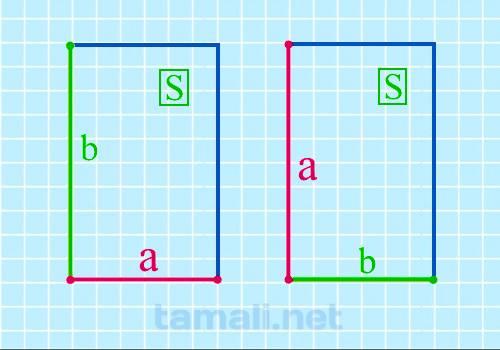
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно

a = S / b

где S — площадь прямоугольника, b — известная сторона.

Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.

Через диагональ и известную сторону

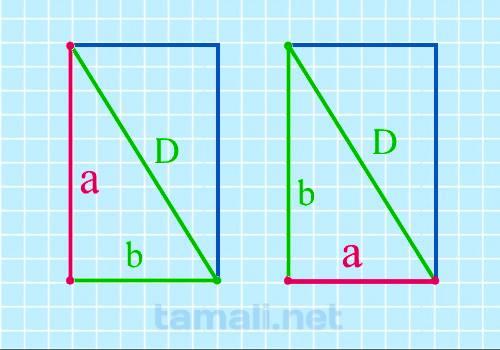
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.Диагональ — это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две соседние стороны — остальные стороны треугольника. Отсюда :

a = √(d² — b²)

где d — диагональ, а, b — стороны.

Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.

Решение. D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см. ​

Через диагональ и угол между диагоналями

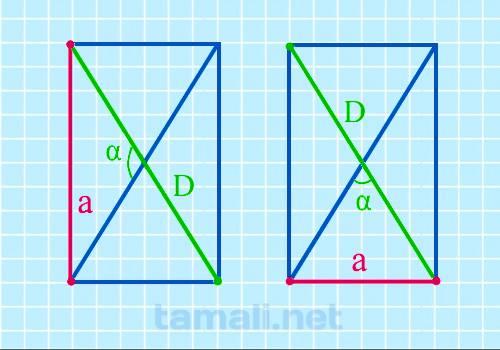
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать сторону прямоугольника, зная следующую формулу:

a = D • sin(α/2)

где D — диагональ, α — угол между диагоналями.

Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти сторону.

Решение. a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.

Через периметр и другую известную сторону

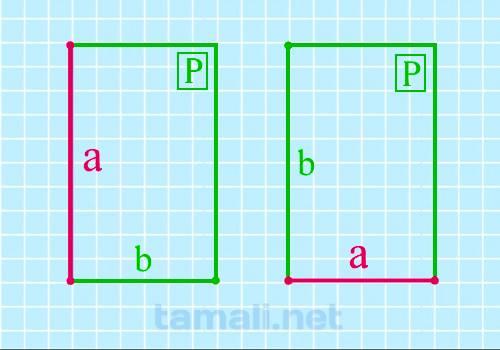
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра для получения длины. P = 2 (a + b).

a = (P — 2b) / 2

где P — периметр прямоугольника, b — другая известная сторона.

Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4) .Вычислив, получим 12 см.

Другие примеры по решению задач на прямоугольник с использованием длины и ширины

1. Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
   Результат: P прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов
2. Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3 м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см. Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см².

Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены ниже.